La diffraction d'électrons de haute énergie en réflexion (RHEED) est particulièrement utilisée pour caractériser la surface in-situ pendant la croissance par EJM. En effet son fonctionnement sous ultra vide et le fait que le faisceau d'électrons soit dirigé parallèlement à la surface (donc perpendiculairement à l'axe de croissance) facilitent son implantation sur un bâti d'épitaxie. La technique RHEED permet notamment de déterminer la reconstruction de la surface, de mesurer la vitesse de croissance et d'apprécier qualitativement la planéité de la surface.

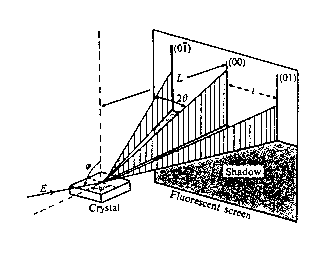
Un dispositif RHEED consiste en un faisceau d'électrons d'une énergie de 10 à 50 keV focalisé sur la surface. La longueur d'onde associée aux électrons est de l'ordre de 0.1 Å. Le faisceau atteint la surface en incidence rasante avec un angle de 1 à 2 degrés (figure I-14).

Figure I-14 : principe du RHEED : On observe sur un écran les figures de diffraction sur les électrons réfléchis et diffractés par les atomes de la surface

Dans cette configuration l'interaction des électrons avec la surface se limite à quelques plans atomiques. Le faisceau qui en résulte est visualisé sur un écran fluorescent. Deux phénomènes importants interviennent lors de l'interaction du faisceau avec la surface : la réflexion et la diffraction.

La réflexion pure du faisceau entraîne la présence d'une tache spéculaire sur l'écran de visualisation. Or l'intensité du faisceau réfléchi est très sensible à la rugosité de la surface. En effet les marches atomiques de la surface diffusent une partie des électrons (la diffusion est une diffraction aléatoire qui ne permet pas la formation d'interférences). Aussi l'intensité de la tache spéculaire est directement liée à la densité de marches sur la surface. Or, lors de la croissance sur un substrat non désorienté, la formation des nucléi et des marches se fait de façon cyclique : Si on part d'une surface idéale, des terrasses nucléent et se développent. Puis les atomes arrivant sur la surface s'incorporent préférentiellement aux terrasses existantes. Lorsque ces terrasses atteignent une taille suffisante elles coalescent pour finalement former à nouveau un plan cristallin complet. Le cycle peut recommencer par la formation de nucléi. Ce cycle peut être observé en suivant l'intensité de la tache spéculaire qui présente des oscillations régulières (figure I-15). Le maximum d'intensité réfléchie correspond au moment où la couche est la plus proche d'un plan cristallin idéal. Le temps séparant deux maxima d'intensité correspond donc au temps de dépôt d'une couche monomoléculaire. Ainsi la mesure du temps séparant deux maxima d'intensité permet de déterminer la vitesse de dépôt.

D'autre part, la diffraction des électrons par le réseau atomique de surface entraîne la formation d'interférences. La visualisation des interférences électroniques sur un écran fluorescent peut être considérée comme une projection de l'espace réciproque. Dans le cas d'une surface plane la faible pénétration des électrons permet de ne considérer que les interactions avec le réseau 2D de surface. Les figures de diffraction observées représentent l'intersection du réseau réciproque de la surface (de paramètre de maille 2p/a où a est la maille du réseau direct) et de la sphère d'Ewald de rayon k où k est le nombre d'onde des électrons du faisceau (k=2p/l). Dans le cas idéal d’une surface parfaitement plane et d’une sphère d’Ewald d’épaisseur nulle, la figure de diffracion serait constituée de points. Cependant la sphère d’Ewald a une épaisseur non nulle liée à la dispersion des électrons du faisceau. Le paramètre de maille de surface est de l'ordre de 4 Å et la longueur d'onde des électrons de l'ordre de 0,1 Å. Le rayon de la sphère d'Ewald est donc grand devant le paramètre du réseau réciproque, et la sphère d'Ewald peut être approximée par un plan (figure I-16). C'est pourquoi la figure de diffraction est constituée de raies parallèles plutôt que de points.

Figure I-15 : oscillations d'intensité de la tache spéculaire liée à la densité de marches

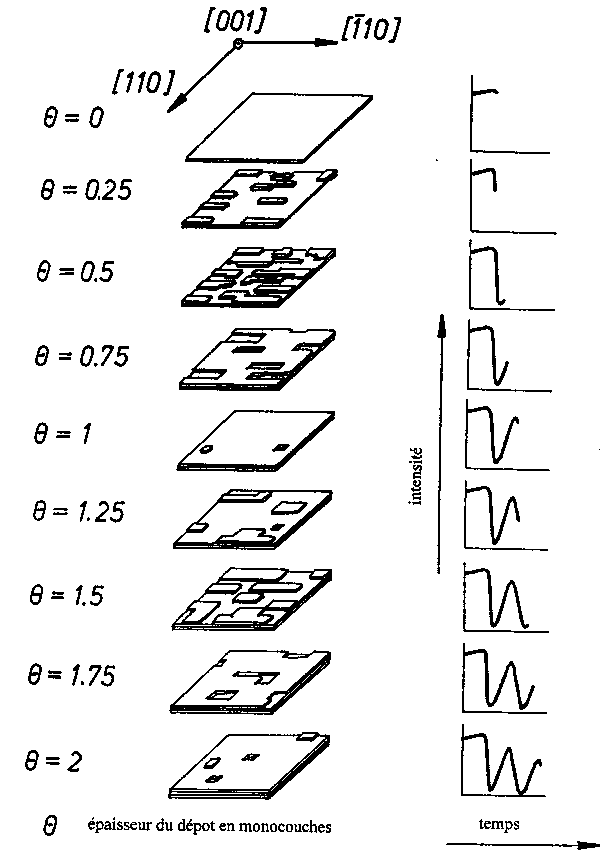
Figure I-16 : intersection de la sphère d'Ewald (SE) avec les lignes du réseau réciproque.

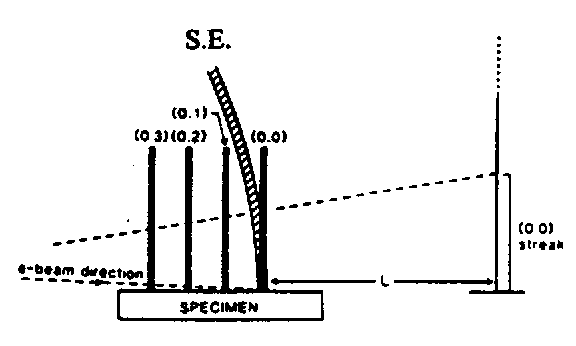
La distance entre deux raies est directement proportionnelle à l'inverse du paramètre de maille de surface dans la direction perpendiculaire au faisceau incident. Le coefficient de proportionnalité dépend des conditions de projection du faisceau, i.e. de la géométrie de l'installation. Les interférences ainsi observées permettent de déterminer la reconstruction de la surface. Il est également possible d'obtenir des informations qualitatives sur la morphologie de la surface : pour une couche parfaitement plane le diagramme RHEED est constitué de raies parallèles (figure I-17a). Lorsque la couche présente une morphlogie tridimensionnelle (3D), une partie du faisceau est transmise à travers les îlots (figure I-17b). Il en résulte une nouvelle interférence de type volumique avec les plans denses du cristal. Ainsi le diagramme RHEED qui est constitué de lignes pour une surface plane se présente sous forme de taches de diffraction pour une surface 3D. Ces taches somment l'intensité des raies observées sur la surface plane. Lorsque des plans cristallins d'orientation différente de l'orientation nominale du substrat se forment sur la surface, les taches s'allongent suivant des directions dont l'orientation est caractéristique de ces nouveaux plans cristallins. Les taches adoptent alors une forme caractéristique en "V" observée notamment lors de la formation de facettes (114) avec un faisceau parrallèle à [1-10].

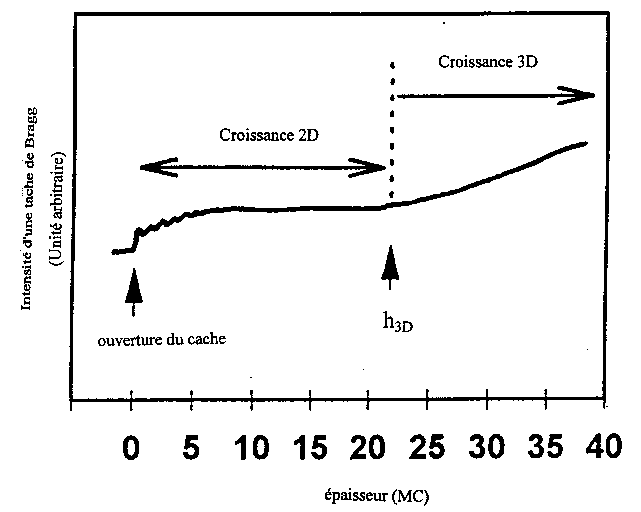
Ainsi l'enregistrement du diagramme de diffraction RHEED pendant la croissance fournit des informations précieuses sur la morphologie de la couche : l'évolution de l'intensité d'une tache de diffraction peut être utilisée pour déterminer avec précision l'épaisseur critique au delà de laquelle la croissance est 3D. On trace l'évolution de l'intensité d’une tache de diffraction en fonction du temps : pour une couche plane l'intensité diffractée est répartie sur toute une ligne, et l'intensité du centre de la tache est faible et approximativement constante (mis à part les oscillations). Lorsque la surface évolue vers une morphologie 3D, les lignes évoluent vers des taches plus intenses. Aussi la rupture de pente de la courbe de l'intensité en fonction du temps marque un changement de mode de croissance et correspond à l'épaisseur critique de transition 2D-3D (figure I-18). C'est l'épaisseur à partir de laquelle se forment des îlots 3D.

SUITE

Figure I-17 : diffraction en fonction de la morphologie

Figure I-18 : détermination de l’épaisseur critique de la transition 2D-3D

SUITE