La microscopie à effet tunnel est une technique de caractérisation de surfaces qui permet de déterminer la morphologie d'une surface conductrice ou semiconductrice. Sa capacité à réaliser des images topographiques avec une résolution atomique font du microscope à effet tunnel (STM) un outil de choix pour l'étude de surfaces épitaxiées car il permet d'imager les marches monomoléculaires et même la reconstruction de la surface. Comme il s'agit d'un instrument de petite taille, il est possible de l'adapter à une enceinte sous ultra-vide connectée à un bâti d'épitaxie. Il permet alors de caractériser les surfaces sans qu'elles soient oxydées par un passage à l'air. Cependant il est nécessaire de refroidir l'échantillon pour l'imager car les céramiques piézo-électriques du STM ne peuvent supporter une température supérieure à 150°C. Il est donc nécessaire de geler la surface à la fin de la croissance afin de la caractériser. Ceci est obtenu par un refroidissement rapide sous flux d'arsenic (cf. chapitre III).

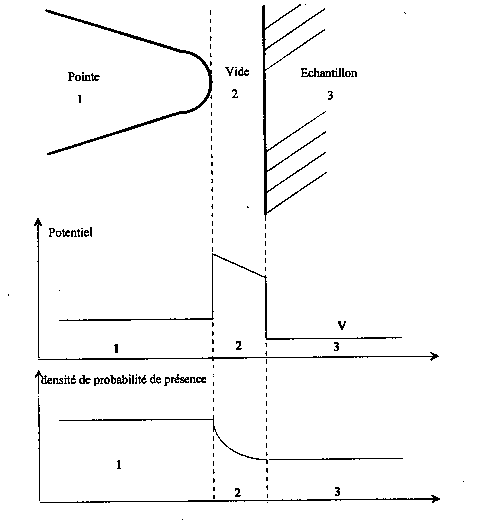
Le microscope à effet tunnel utilise le phénomène quantique de franchissement d'une barrière de potentiel par des électrons (figure I-19).

Figure I-19 : couplage entre les états électroniques

Une pointe (1) et une surface conductrice (3) séparées par un espace vide (2) constituent deux milieux où les électrons circulent librement, séparés par une barrière de potentiel due au travail de sortie des électrons. Lorsque la distance qui sépare la pointe et l'échantillon est de l'ordre du nanomètre, un couplage décrit par la mécanique quantique s'établit entre les orbitales électroniques de la pointe et de la surface à imager : la densité de probabilité de présence des électrons originaires de la pointe n'est pas nulle dans l'échantillon. Lorsqu'on impose une différence de potentiel (de l'ordre de 0.1 à 4V) entre la pointe et la surface un courant (de l'ordre de 0.1 à quelques nanoampères) s'établit. Le principe du microscope à effet tunnel repose sur la mesure et la régulation de ce courant tunnel lors du balayage de la surface par la pointe (figure I-20). Le positionnement respectif de la pointe et de l'échantillon est assuré par des céramiques piézo-électriques (dont la maille cristalline se déforme lorsqu'on applique une différence de potentiel). Elles permettent un contrôle du positionnement à une fraction d'angström près. On effectue un balayage de la surface de l'échantillon par la pointe alors que la distance pointe-échantillon est maintenue constante par régulation du courant tunnel. En enregistrant la réponse de la boucle de régulation on obtient une image directe de la topographie de la surface. Le premier microscope à effet tunnel fut mis au point par Binnig et Rohrer [54, 55] qui obtinrent pour cela le prix Nobel de physique en 1986.

Plusieurs modèles ont permis de calculer théoriquement le courant tunnel en prenant en compte la forme de la pointe. On peut citer en particulier l'étude de Tersoff et Hamman [56, 57] qui permet de calculer le courant tunnel lorsque la pointe est à symétrie sphérique, c'est à dire qu'elle se présente sous la forme d'une orbitale de type s. L'expression du courant tunnel obtenue est :

avec :

où e est la charge de l'électron,

V est la différence de potentiel appliquée entre la pointe et l'échantillon,

R est le rayon de courbure de la pointe,

f est le travail de sortie pour un électron,

r(r₀,E_f) est la densité d'états électroniques de la surface au centre de courbure de la pointe au niveau de Fermi,

D_p(E_f) est la densité d'états électroniques de la pointe au niveau de Fermi.

Ce modèle a permis de montrer que l'image de la surface donnée par la microscopie tunnel correspond à un contour d'isodensité d'états au niveau de Fermi. De plus l'expression des densités d'états en fonction de la distance permet de montrer que le courant tunnel diminue exponentiellement avec la distance pointe-échantillon. Dans ces conditions si la pointe se termine par un atome plus proche de la surface que les autres on peut montrer que plus de 90% du courant passe par le dernier atome de la pointe. Grâce à cela la résolution spatiale du STM peut atteindre une échelle subnanométrique. C'est pourquoi il est possible de résoudre la position des atomes sur une surface. Ceci est obtenu couramment avec du graphite qui permet de tester le microscope, mais également sur des surfaces métalliques ou semiconductrices, où la corrugation (variation de hauteur enregistrée par la pointe entre deux atomes) est de l'ordre de 0.1Å. On remarquera que la pointe est un élément essentiel du microscope à effet tunnel. Ces pointes sont réalisées par affûtage chimique à partir de fils de tungstène ou de platine-irridum. L'extrême finesse de la pointe la rend extrêmement fragile. Elle peut être irrémédiablement détériorée par tout contact, et en particulier avec l'échantillon à imager. Lors d'un choc avec l'échantillon (lors de la procédure d'approche de la pointe par exemple) elle peut se courber, et son extrémité devient extrêmement sensible aux vibrations mécaniques, ce qui peut empêcher la régulation du courant tunnel. D'autre part lorsque le rayon de courbure de la pointe est grand il est possible que les images obtenues sur des surfaces présentant d'importantes variations de hauteur soient affectées. En effet une pointe trop "émoussée" ne pourra pas suivre la morphologie de la surface de façon aussi précise qu'une pointe fine. L'image obtenue résulte alors de la convolution de la forme de la pointe et de la surface. La pointe est donc l'élément clé du microscope et le plus grand soin est consacré à son élaboration ainsi qu'à sa manipulation. Cependant si la pointe est sous vide (et par conséquent protégée contre toute contamination) et si elle ne subit pas de choc, sa durée de vie peut être assez grande.

SUITE : Chapitre II Dispositif expérimental