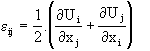
IV Calculs des déformations et des contraintes
L'étude des contraintes et des déformations fait l'objet de la mécanique des milieux continus[53 par exemple]. Nous allons utiliser la théorie de l'élasticité linéaire en petites déformations et nous rappelons ici quelques éléments de cette théorie. Soit Ui le champ des vecteurs de déplacement. On considère le tenseur des déformations linéarisées eij, défini par :
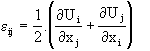
Le champ des contraintes est décrit par le tenseur sij.
Dans le cas statique, l'équilibre des forces dans le matériau s'écrit :
![]()
La loi de comportement du matériau donne la relation liant le tenseur des contraintes et le champ des déplacements. Pour un matériau élastique isotrope la relation entre le tenseur des déformations e et le tenseur des contraintes s s'écrit :
![]()
![]()
![]()
![]()
où Y est le module d'Young, n le coefficient de Poisson et m le module de cisaillement du matériau. Les constantes élastiques des alliages InGaAs peuvent être calculées par interpolation linéaire à partir des constantes de GaAs et InAs (tableau 1) [16].
Tableau 1
|
|
Module d'Young |
Coef.de Poisson |
|
InAs |
79 GPa |
0,35 |
|
GaAs |
124 GPa |
0,31 |
|
In1-xGaxAs |
124.x+79.(1-x) |
0,31.x+0,35.(1-x) |
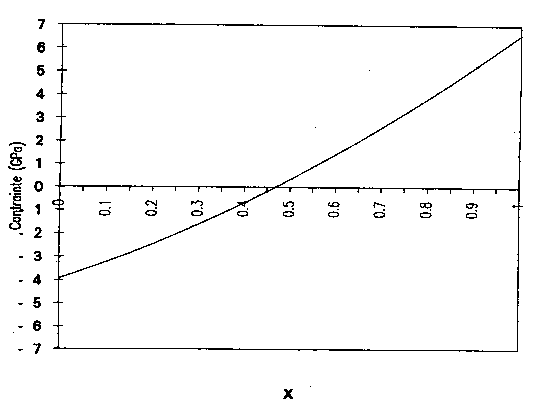
Figure I-12 : contraintes d'une couche 2D en fonction de la composition x en gallium
Contraintes et déformations doivent être calculées en tenant compte des conditions aux limites. Il peut s'agir soit de déplacements, soit d'efforts appliqués ou encore de certaines composantes du déplacement et des composantes complémentaires des efforts. Le problème consiste à déterminer les champs de contraintes et de déformations en résolvant le système d'équations différentielles donné par la relation de la statique, la loi de comportement et les conditions aux limites imposées sur les bords du matériau.
Dans le cas d'une couche 2D plane et sans défauts, le calcul des champs de déformations et de contraintes est très simple car ces champs sont uniformes. La condition aux limites à l'interface entre le dépôt et le substrat est l'égalité des paramètres de maille dans le plan de l'interface. Si le substrat est assez épais son paramètre de maille ne change pas. On peut alors calculer simplement les contraintes dans la couche déposée. Soit e// la déformation dans la direction parallèle au substrat et e^ la déformation dans la direction de croissance.
On a :
![]()
La condition aux limites naturelle sur la surface libre est que la composante de la contrainte orthogonale à l'interface est nulle. Les lois de comportement élastique donnent :
![]()
![]()
Les valeurs des contraintes en fonction de la composition sont reportées sur la figure I-12. On voit que les valeurs de contraintes que l'on peut atteindre dépassent largement la limite élastique en volume qui est de l'ordre de la centaine de MPa. Ceci est possible car la plasticité est une propriété macroscopique des matériaux qui résulte de la propagation et de la multiplication des dislocations. Dans le cas d'une couche mince où les dislocations sont trop coûteuses en énergie pour être formées, les propriétés plastiques du matériau sont considérablement modifiées.
Dans le cas d'une surface formant des îlots, les champs de déformation et de contraintes ne sont pas uniformes. La résolution des équations différentielles est alors plus délicate. La recherche des solutions peut être facilitée par une formulation variationnelle du problème. La théorie des formulations variationnelles permet de montrer que la recherche des solutions du système d'équations différentielles précédemment décrit revient à un calcul de minimisation d'énergie potentielle sur l'espace des champs de contraintes compatibles avec les conditions au limites de type cinétique. On peut alors se restreindre à un espace de champs de contraintes de dimension finie afin de calculer une solution approchée. C'est le principe de base de la méthode de calcul par éléments finis.