Le paramètre de maille d'un composé III-V dépend de sa composition : les paramètres de maille respectifs de InP, GaAs et InAs sont a_InP=5,8687 Å, a_GaAs=5,6533 Å, a_InAs=6,0583Å. Le paramètre de maille d'un alliage InGaAs non contraint est déterminé par une loi linéaire (de Vegard) en fonction de la proportion de gallium et des paramètres de maille des composés binaires non contraints InAs et GaAs [16]. Le paramètre de maille de l'alliage In_1-xGa_xAs est donné par :

a_x=a_GaAs.x+a_InAs.(1-x)

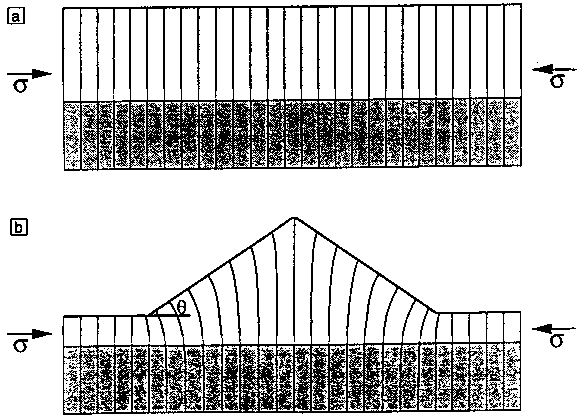
Ainsi In_1-xGa_xAs a le même paramètre de maille que InP pour x=0,468. Pour d'autres valeurs de x lors de l'épitaxie de In_1-xGa_xAs sur InP le raccordement des mailles à l'interface entraîne l'existence d'une déformation de la maille cristalline (figure I-8).

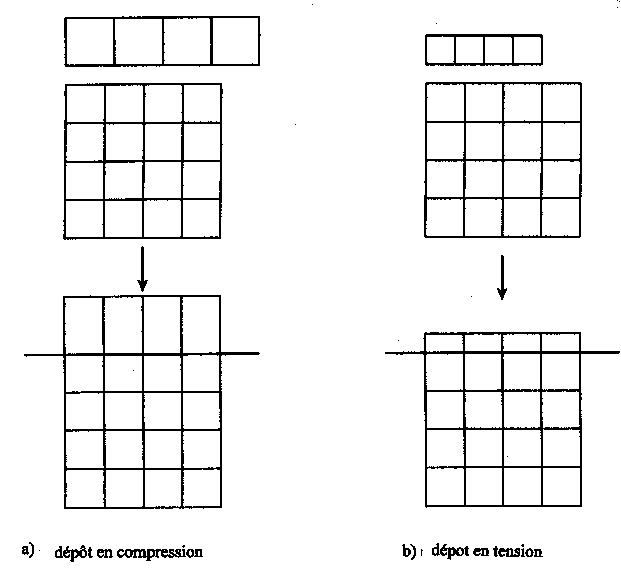
Figure I-8 : contraintes dues aux différences de paramètres de maille

Il en résulte des contraintes élastiques dans le dépôt. Les couches InGaAs sur InP présentent la particularité de pouvoir être contraintes soit en compression (figure I-8a) soit en tension (figure I-8b) selon que leur composition est respectivement riche ou pauvre en indium. La déformation correspond à une compression (déformation négative) si le paramètre de maille de la couche déposée est supérieur à celui du substrat, et à une tension (déformation positive) si le paramètre de maille de la couche déposée est inférieur à celui du substrat. Ces contraintes entraînent l'existence d'une énergie de déformation de la couche épitaxiée. Afin de minimiser cette énergie les contraintes ont tendance à se relaxer. Le mode de relaxation de contraintes le mieux connu pour les couches épitaxiées est la relaxation plastique caractérisée par la formation de dislocations à l'interface [17-26] : L'introduction de dislocations entraîne une modification du paramètre de maille de la couche déposée et les contraintes élastiques peuvent être relaxées (figure I-9).

Figure I-9 : relaxation par dislocations

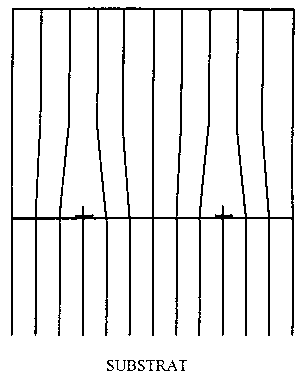
Cependant la formation d'une dislocation nécessite un apport d'énergie. Lorsque l'épaisseur de la couche déposée est de l'ordre de quelques monocouches, l'énergie élastique accumulée est inférieure à l'énergie qu'il faut fournir pour créer des dislocations. Les système n'a alors aucun intérêt à former des dislocations coûteuses en énergie. Cependant lorsque la couche déposée atteint une épaisseur critique, la formation des dislocations devient énergétiquement favorable. Cette épaisseur critique a été déterminée expérimentalement en fonction du désaccord des paramètres de mailles dans différents systèmes et en particulier pour des dépôts InGaAs/InP [27]. Plusieurs modèles permettent de la calculer. Le plus fréquemment invoqué est le modèle de Matthews et Blakeslee [28] basé sur l'équilibre entre la tension de ligne d'une dislocation et la contrainte de volume. Dans ce modèle l'épaisseur critique h vérifie la relation :

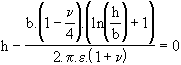
où b est le vecteur de Burgers de la dislocation, e le désaccord de maille et n le coefficient de Poisson.

Un autre mode de relaxation, lié à la formation d'une morphologie tridimensionnelle ou rugueuse a été largement observé [29-41]. Lorsque des îlots se forment sur la surface la répartition des contraintes n'est plus uniforme. En effet les côtés de ces îlots constituent une surface libre qui peut permettre aux mailles cristallines de se déformer (figure I-10).

Figure I-10 : Relaxation dans les îlots

a) couche contrainte biaxialement

b)Le paramètre de maille peut se relaxer partiellement sur les surfaces libres constituant les flancs des îlots.

Ainsi une croissance sous forme d'îlots cohérents (croissance de type Stranski Krastanov) peut permettre de relaxer partiellement les contraintes élastiques. Cette croissance de type Stranski-Krastanov induite par la contrainte peut se produire avant la formation de dislocations et constitue alors une alternative à la relaxation plastique. Les premiers modèles mécaniques macroscopiques montrant qu'une surface plane d'un matériau contraint biaxialement dans le plan de la surface est instable sont dus à Asaro-Tiller [42] et Grinfeld [43]. Ces modèles ont été développés pour le cas de l'interface d'un liquide avec un solide contraint de façon non hydrostatique, et ont été appliqués plus tard au cas de couches minces de semiconducteurs. Les hypothèses concernant la forme sinusoïdale de la surface dans ces modèles ne peuvent pas s'appliquer aux surfaces à marches d'un monocristal, cependant des calculs considérant une surface formée de marches ou de facettes cristallines ont montré que dans ce cas également une morphologie tridimensionnelle sous forme d'îlots correspond à une configuration énergétiquement plus stable qu'une surface plane [44-46]. On peut encore désigner sous le nom d'instabilité d'Asaro-Tiller-Grinfeld (ATG) la formation d'une morphologie tridimensionnelle (3D) par la relaxation élastique des contraintes. L'énergie de relaxation élastique d'un solide, E_r, est définie comme la différence entre l'énergie E_e0 d'une quantité de matière entièrement contrainte au paramètre de maille du substrat et l'énergie élastique E_e de la même quantité de matière sous forme d'îlot (i.e. partiellement relaxée) :

E_r=E_e0-E_e

La répartition exacte des contraintes dans l'îlot, et par conséquent l'énergie de relaxation élastique dépendent de la forme de ses côtés libres. De façon générale l'énergie de relaxation élastique est proportionnelle à E_e0 :

Er=aE_e0

Le coefficient de proportionnalité a dépend de la forme de l'îlot et peut être calculé par la mécanique des milieux continus. La formation d'un îlot entraîne une augmentation de la surface libre du matériau sur les flancs de l'îlot. Donc l'énergie de surface E_s du matériau, s'en trouve augmentée d'une valeur DEs liée à l'augmentation de la surface libre. Prenons pour référence une couche 2D du matériau contraint. La formation d'un îlot entraîne une diminution de l'énergie élastique de volume, Er, et une augmentation de l'énergie de surface. La variation de l'énergie totale DE_3D est donc égale à :

Si l'énergie de relaxation élastique dans un îlot est inférieure à l'énergie de surface supplémentaire (due aux flancs) alors la morphologie 2D est stable car la création de la morphologie 3D nécessiterait un apport d'énergie. Si l'énergie de relaxation élastique est supérieure à l'énergie de création des surfaces libres, alors la morphologie 3D est énergétiquement plus stable que la morphologie 2D. Considérons pour simplifier le cas d'un îlot parallélépipédique de hauteur h, de largeur l dans la direction Ox et de longueur L dans la direction Oy :

L'énergie de relaxation élastique s'écrit :

Où e est la déformation due au désaccord de maille, Y le module d'Young du matériau et a un coefficient de proportionnalité. Si g_x,y,z est l'énergie spécifique d'une surface orthogonale à Ox, Oy, Oz respectivement, l'énergie de surface de l'îlot est :

Alors l'augmentation de l'énergie de surface du système associée aux flancs latéraux d'un îlot est :

On obtient pour condition de stabilité de la morphologie 3D :

ce qui donne

et

Ainsi les îlots ne seront stables que si leur dimension latérale dépasse une valeur critique. Les calculs de Grinfeld [43] ont montré que ce résultat est général : sur la surface d'un matériau contraint toute ondulation de longueur d'onde supérieure à une longueur critique L se développe, alors que les ondulations de longueur d'onde inférieure à L ne sont pas stables. Dans le cas d'une surface continue (sinusoïdale) cette longueur critique est donnée par la relation [43,47-48]:

où s₀ est la contrainte dans une couche 2D et g l'énergie spécifique de surface du matériau. Ainsi les îlots sont stables si leur taille est supérieure à une taille minimale proportionnelle à l'énergie de surface. C'est pourquoi un matériau ayant une grande énergie superficielle est, d’une manière générale, défavorable au développement d'une morphologie 3D (le mode de croissance 3D crée des surfaces libres). D'autre part la taille minimale est inversement proportionnelle au carré de la contrainte. Pour de faibles contraintes, la taille minimale devient très grande et est difficile à atteindre. Cependant de grands îlots sont toujours plus stables qu'une couche plane contrainte.

Il faut noter que ces considérations sont d'ordre énergétique et déterminent dans quel cas la formation des îlots est thermodynamiquement possible. Or la formation de la morphologie 3D peut être influencée par des paramètres cinétiques [49-52]. Orr et al. [41] suggèrent que la cinétique est très importante dans la formation de la morphologie de la surface. On comprend bien par exemple que si la thermodynamique indique que de grands îlots sont toujours plus stables qu'une couche plane contrainte, leur formation nécessite des conditions cinétiques qui ne seront pas forcément atteintes (comme une très grande longueur de diffusion), et qu'en pratique ces grands îlots ne seront pas observés. Ceci explique que les paramètres qui déterminent l'épaisseur critique de la transition 2D-3D soient encore largement discutés.

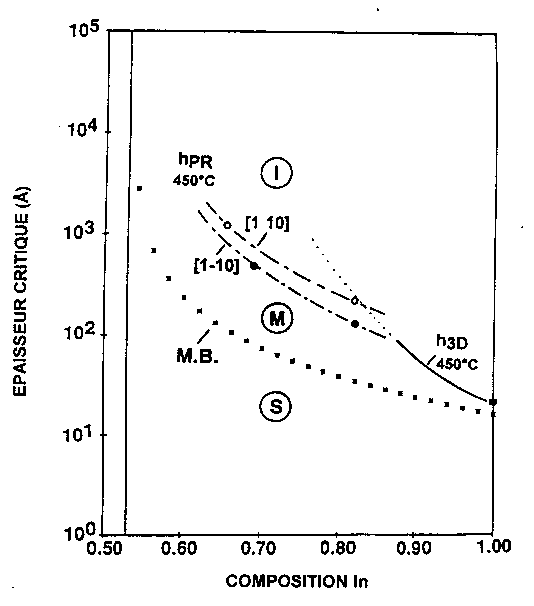
Dans le système In_1-xGa_xAs sur In_0,53Ga_0,47As sur InP, on observe une transition 2D-3D pour des couches contraintes en compression (x<0,47) lorsque la différence de paramètre de maille est supérieur ou égal à une valeur de l'ordre de 2% (x=0,18). L'épaisseur du dépôt à partir de laquelle se forme une morphologie 3D est appelée épaisseur critique de la transition 2D-3D et est notée h_3D. Cette épaisseur critique dépend de l'amplitude de la contrainte, mais aussi des conditions de croissance de la couche (température, vitesse de croissance) : Pour une contrainte en compression à 2% d'écart de maille la transition 2D-3D est observée à la température de croissance de 525°C alors que pour une température de 450°C la formation de dislocations a lieu avant la transition 2D-3D (Figure I-11)[27].

Pour des couches contraintes en tension, peu d'informations sont disponibles en ce qui concerne la transition 2D-3D. La comparaison de la transition 2D-3D en fonction du signe de la contrainte constitue justement l'une des originalités de notre étude.

SUITE

Figure I-11 : Courbe des épaisseurs critiques pour InGaAs sur InP à 450°C en fonction de la composition en indium. La courbe M.B. correspond au modèle de Mattews et Blakeslee. Les courbes h_PR correspondent à la mesure expérimentale de l'épaisseur à laquelle se forme les dislocations dans les directions [110] et [1-10] respectivement. La courbe h_3D correspond à la formation d'une morphologie rugueuse (3D).