Deux types de sollicitations mécaniques peuvent être distinguées sur le système sous ultra vide : les vibrations continues dues aux pompes et aux autres appareils électriques, et les sollicitations transitoires dues à des chocs ou à des manipulations de vannes. Les principales sources de vibrations et de bruit acoustique sont quatre pompes turbomoléculaires qui fonctionnent en permanence ainsi qu'un système de climatisation. La contribution d’autres appareils aux vibrations est apparue nettement plus faible. Les vibrations continues ont été mesurées sur l’enceinte du microscope à l’aide d’un accéléromètre piézo-électrique. Les accélérations ont été enregistrées pendant quelques secondes et les spectres de fréquences ont été obtenus par transformée de Fourier en utilisant une fenêtre de Hanning pour minimiser les pics secondaires dus au fenêtrage : avant la transformation, le signal a été multiplié par la fonction

où t est la coordonnée de temps telle que la durée de la mesure s’étend entre t=-T/2 et t=T/2. On définit un système de coordonnées cartésien : les axes Ox et Oy sont dans le plan horizontal correspondant au plan de l’échantillon, et l’axe vertical Oz correspond à l’axe de la pointe du microscope. Des spectres d’accélération en fonction de la fréquence présentent les mêmes fréquences mais différentes amplitudes suivant les trois directions (figure II-7). Des maxima sont mesurés pour des fréquences de 24 Hz, 50 Hz et 100 Hz. Cependant les amplitudes de déplacement sont plus pertinentes pour cette étude où les déplacements pointe-échantillon sont déterminants. Les amplitudes d’accélération ont donc été converties en amplitudes de déplacement Dz par la relation :

où f est la fréquence. L’amplitude maximale obtenue est de 0.6 microns à la fréquence de 50 Hz dans la direction Oz. Des déplacements comparables sont obtenus à des fréquences plus faibles malgré l’amplitude d’accélération plus faible. En effet à basse fréquence de faibles accélérations peuvent correspondre à des déplacements importants. Les sollicitations mécaniques sont donc importantes, en particulier à basse fréquence, et il a été nécessaire d'étudier avec attention leur isolation avant l'implantation d’un microscope à effet tunnel.

Des mesures effectuées au sous-sol ne montrent pas de sollicitations au delà de 1 Hz (insert figure II-7). Pour des fréquences plus basses l’accéléromètre n’est plus fiable et le pic vers 0 Hz est un artefact de mesure. Ce sous-sol est un bon endroit pour implanter un microscope à effet tunnel et nous avons choisi d’y installer le socle de notre installation.

Afin d'évaluer les performances du système d'isolation des vibrations que nous avons conçu, nous allons le modéliser et calculer sa fonction de transfert pour les vibrations.

Nous allons calculer la fonction de transfert du système en deux étapes successives, en modélisant séparément le système d’isolation et le microscope. Ces modèles sont utilisés pour calculer la fonction de transfert pour les vibrations et permettent une évaluation théorique des performances du système [7].

Le système d’isolation précédemment décrit peut être modélisé par un système masses-ressorts (figure II-8). Seules les translations sont à prendre en compte car elles présentent les amplitudes de déplacement de loin les plus importantes. Un modèle identique est utilisé dans les trois directions de l’espace.

Le soufflet déformable a d'abord été modélisé à l'aide du logiciel ANSYS [8] (logiciel de simulation numérique de systèmes mécaniques) afin de déterminer ses fréquences de résonances. La première fréquence de résonance calculée est de 6,6 Hz suivant Ox et Oy (mode de flexion) et de 13,4 Hz suivant Oz (mode de traction-compression). Les fréquences de résonances suivantes sont des harmoniques de la première. Dans le modèle masse-ressorts, le soufflet déformable est modélisé par un ressort de raideur Ks,z =1000N/m dans la direction Oz et Ks,x = Ks,y = 918N/m dans les directions Ox et Oy. Ces valeurs données par le fabricant sont en bon accord avec les résultats des simulations numériques. L’amortissement supplémentaire mis en place autour du soufflet n’introduit pas de modification significative dans le calcul de la fonction de transfert du système en dehors des fréquences de résonance à cause de la rigidité du support.

Le trépied métallique peut être modélisé par une masse M_t,i (avec i = x, y or z) et un ressort de raideur K_t. L’extrémité du ressort liée à la dalle de béton est supposée immobile, et l’autre est reliée à la masse M_t,i. Cette masse représente la somme de la masse mobile du trépied, de la masse du microscope et de la masse de la bride de fixation et des barres métalliques très rigides liant la bride au trépied. L’évaluation de la masse mobile du trépied est délicate car le trépied forme un système encastré-libre très hyperstatique. Aussi une simulation numérique a été effectuée pour évaluer cette masse mobile suivant la direction de sollicitation. En effet le trépied n’étant pas symétrique, sa masse mobile n’est pas la même dans toutes les directions. De façon à obtenir un modèle aussi réaliste que possible, la raideur Kt,i (avec i = x, y or z) modélisant le trépied a été déterminée de façon semi-empirique : les fréquences de résonance f0 dans chacune des trois directions ont été mesurées à l’aide d'un accéléromètre piézo-électrique et la raideur a été calculée à partir de ces fréquences de résonance en utilisant l’équation:

(2pf0)2= Kt,i/Mt,i.

A partir de ce modèle il est possible de calculer la fonction de transfert F du système d’isolation. Soient Dx, Dy, Dz les amplitudes des vibrations dans les directions respectives Ox, Oy, Oz sur la chambre à vide reliée au bâti d’épitaxie et Dx_t Dy_t Dz_t les amplitudes des vibrations transmises à la bride du microscope fixée sur le trépied. La fonction de transfert F est calculée à partir de la loi fondamentale de la dynamique :

avec et .

On obtient les fonctions de transfert dans les directions Ox et Oy en remplaçant Ks,z par Ks,x (ou Ks,y ), Kt,z par Kt,x (ou Kt,y ) et Mt,z par Mt,x (ou Mt,y). Les résultats numériques sont présentés dans le tableau 1.

Tableau I

En effectuant un calcul de l’amplitude transmise à partir de l’amplitude la plus importante mesurée sur la chambre à vide i.e. 0,6 microns à 50 Hz on obtient un déplacement de la base du microscope d’une amplitude de 8 10^-11 m dans la direction Oz. De même on calcule des amplitudes de 1.3 x 10^-10m dans la direction Ox et. 2.2 x10^-10 m dans la direction Oy.

Le diagramme de Bode de la fonction de transfert du système d’isolation est présentée figure II-9. Ce système d’isolation présente l’avantage d’avoir une très faible valeur de la fonction de transfert en dessous de la première fréquence de résonance. Il constitue une alternative intéressante à la suspension à un ou deux étages par des ressorts ou à une suspension pneumatique [2, 5, 9-10]. En effet un système de suspension est très efficace pour des fréquences supérieures à la première fréquence de résonance, mais il est inefficace pour des fréquences inférieures. La suspension à deux étages nécessite l'utilisation de grands ressorts pour diminuer au maximum cette fréquence de résonance. Elle est donc difficilement utilisable dans une enceinte sous vide. Dans le cas d’une suspension avec une première fréquence propre de 5Hz, la fonction de transfert a un gain nul en dessous de 5Hz et égal à -40dB à 50Hz. Dans notre cas nous avons calculé un gain de -80dB à 50 Hz et en deçà avec l’avantage d’un gain faible aux basses fréquences.

Afin de calculer sa fonction de transfert, le microscope est modélisé par un système masses-ressorts (figure II-10). Soit m_e la masse du porte échantillon (m_e=28g) et m_b la masse de la base du microscope (m_b=66g). Soient Kp et K'p les raideurs des tubes piézo-électriques en traction compression et en flexion respectivement. Ces raideurs sont obtenues à partir d’un calcul de raideur de poutres [11] :

Kp = p.d.e.Y / l

suivant Oz et

K'p = 3 Y.J / l3 avec suivant Ox et Oy

où l est la longueur du tube, d son diamètre extérieur et e l’épaisseur de la céramique. Y et J sont respectivement le module d’Young de la céramique et le moment d’inertie de la poutre. Avec Y=66 Gpa [12], l=10 mm, d=2,25 mm, e=0,5 mm on obtient K_p=2,33.10⁷ N/m et K’_p=2,23.10⁵N/m. La base de l'assemblage tunnel repose sur trois plots en Viton. Chaque plot est modélisé par un ressort de raideur K_a en parallèle avec un amortisseur pur. Avec une valeur approximative de 21 MPa pour le module d’Young du Viton [13], on obtient K_a=4,4.10⁴ N/m et K’_a=3660 N/m. Une estimation du coefficient d’amortissement à partir de l’atténuation d’une oscillation donne a_a=15 N.s/m suivant Oz et a_a'=1,3 N.s/m suivant Ox et Oy. Ces valeurs ne sont qu’une approximation car le coefficient d’amortissement dépend de la fréquence de sollicitation [2].

La forme de la pointe du STM dépend fortement de ses conditions de fabrication. Une pointe idéale avec un atome à son extrémité peut être modélisée comme une poutre droite. Les premières fréquences de résonances calculées sont de 15,9 kHz suivant Ox et Oy et 738 kHz suivant Oz. Cependant ces fréquences de résonance peuvent être considérablement abaissées par la forme non idéale de la pointe.

Soit G la fonction de transfert du microscope pour les vibrations dans la direction Oz. L’étude dans la direction Oz est la plus importante pour l’imagerie car c'est la direction dans laquelle la plus grande stabilité est requise [14]. On utilise une notation complexe pour les amplitudes de déplacement. Soit Dze l’amplitude complexe de déplacement suivant Oz et z_0e l’ordonnée de l’échantillon au repos. On a:

ze= z0e + Re (Dze.ei2pft)

Dans la direction Oz la déformation du tube piézo-électrique supportant la pointe peut être négligée car c'est la direction de l'axe du tube. Les mouvements de la pointe sont donc identiques aux mouvements de la base du microscope. La fonction de transfert du microscope est égale au rapport de l’amplitude du déplacement pointe-échantillon par l’amplitude la sollicitation sur la bride de connexion.

En appliquant l’équation fondamentale de la dynamique aux déplacements de la base du microscope et de l’échantillon, on obtient :

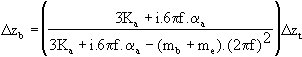et

Et l'expression de la fonction de transfert du microscope est :

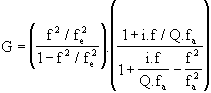
avec , et .

Les valeurs numériques sont données dans le tableau II.

Le tube piézo-électrique central supportant la pointe présente une première fréquence propre en flexion f_p’ estimée à 4,4 kHz à partir d’un calcul de poutre. L’expression de la fonction de transfert G' suivant Ox et Oy est similaire à G pour des fréquences inférieures à cette fréquence propre. Pour des fréquences plus élevées, les sollicitations peuvent causer une excitation de ce tube et il est alors nécessaire de tenir compte de ses déformations. La fonction de transfert G' est alors égale à :

où Dx_p est l'amplitude de déformation de l'extrémité de la pointe.

Le calcul de la fonction de transfert donne:

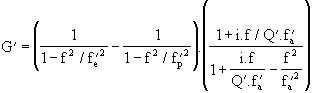
avec , et .

Les valeurs numériques sont données dans le tableau II.

Tableau II : facteur de qualité et fréquences de résonance du microscope.

La fonction de transfert du système (figure II-11) est du type "passe bande". Les pics aux basses fréquences F_a et F'_a correspondent aux fréquences propres de la base du microscope reposant sur les amortisseurs Viton. Les pics à plus haute fréquence F_e correspondent aux fréquences propres de l’assemblage tunnel. Ils ne sont pas amortis car les tubes présentent un amortissement très faible qui n’a pas été pris en compte. Suivant Ox et Oy on note la présence du pic F_p à 4,4 kHz du tube supportant la pointe. L’étude des variations de la fonction de transfert montre qu'une augmentation de la séparation des fréquences de résonance peut permettre de diminuer le gain de la fonction de transfert. Ceci peut être obtenu en diminuant la masse du porte échantillon. Diviser par 3 la masse du porte échantillon permet d’obtenir une diminution du gain de 10 dB.

La fonction de transfert du système total (figure II-12) donne la variation de la distance entre la pointe et l'échantillon à partir de l’amplitude d’une sollicitation sur le bâti d’épitaxie. Elle est obtenue en multipliant la fonction de transfert du système d’isolation avec celle du microscope. Les fréquences de résonance les plus basses F_t et F_t’ sont celles du système d’isolation. Ces pics sont très pointus même en considérant l’amortissement du soufflet. Ils ne pourraient être atténués que par un amortissement du trépied. L’amplitude maximale calculée pour les déplacements pointe-échantillon (avec un porte-échantillon de 28g) à partir du maximum de sollicitation (6 10^-7 m) à 50 Hz sur le bâti d’épitaxie est de 5,6 10^-12 m suivant 0x et 2,5 10^-15 m suivant Oz. Ces valeurs sont nettement inférieures à des amplitudes pouvant perturber les mesures. Dans un deuxième temps les transferts ont été modifiés afin de déposer une masse de 3g sur le STM. Les amplitudes de déplacement transmises à partir du bâti d'épitaxie sont donc encore plus faibles dans la configuration actuelle. Ce système d’isolation est donc particulièrement efficace en l’absence de résonances. Cependant le modèle que nous avons étudié ne tient compte que de la première fréquence propre de chaque constituant du système. En particulier le soufflet présente des fréquences propres de l’ordre de 6 Hz ainsi que de nombreuses harmoniques. Les modes propres correspondants sont susceptibles d’être excités et favorisent la transmission des sollicitations à ces fréquences.

Les performances du microscope avec son système d’isolation ont été testées sur plusieurs types de surfaces sous ultra vide : Elles ont été testées sur une surface de graphite HOPG (figure II-13), sur un dépôt d'or sur mica puis des couches minces InGaAs épitaxiées en accord de maille sur un substrat InP d’orientation nominale (001), sur lesquelles des images de la reconstruction (2x4) ont pu être obtenues. Les images ont été obtenues en mode courant constant, toutes les pompes étant en fonctionnement et de nombreuses autres personnes travaillant simultanément sur le bâti d’épitaxie et le système sous ultra-vide.

Bien que des images de qualité acceptable aient été obtenues dans ces conditions (c'est à dire avec un porte-échantillon lourd de 28g) on constate que le bruit résiduel peut être estimé à 0,1 Å et est supérieur à la valeur calculée précédemment. Afin de déterminer les fréquences des perturbations restantes, les mouvements pointe-échantillon ont été enregistrés en l’absence de balayage sur un échantillon de graphite. En effectuant une transformée de Fourier on voit nettement se détacher les fréquences propres du microscope (figure II-14).

Le pic le plus important se situe à 720 Hz, ce qui est en bon accord avec la fréquence de 780 Hz calculée pour l’assemblage tunnel. Ceci montre l’existence d’un couplage entre les sollicitations suivant Ox et Oy et les perturbations suivant Oz, dont le modèle ne tient pas compte. Cependant les excitations ne sont pas des vibrations mécaniques car les mesures n’ont pas mis en évidence de sollicitations à des fréquences supérieures à 300 Hz. En revanche, en plus des vibrations mécaniques transmises au bâti d’épitaxie, les pompes occasionnent un important bruit acoustique : un bruit acoustique de 65 dB a été mesuré à proximité du bâti d’épitaxie, ce qui correspond à une variation de pression acoustique de 3,5.10^-2 Pa. La force résultante sur la bride STM est difficile à déterminer précisément car elle dépend à la fois des formes du soufflet et du trépied et de la position de la source de bruit. Si on suppose que cette pression s’applique sur la bride supportant le microscope sur une surface correspondant à la section du soufflet, on obtient une force de 1,4 10^-3 N. Or l’amplitude maximale de vibration mesurée sur le bâti d’épitaxie occasionne une force sur la bride supportant le microscope de 6 10^-4 N. La transmission de vibrations acoustiques de l’air est donc déterminante. Ces excitations ne sont pas atténuées par le système d’isolation. Elles peuvent occasionner des excitations des modes propres de vibration du soufflet ou du trépied. Le soufflet qui est l’élément clé du système d’isolation présente de nombreuses fréquences propres qui peuvent être excitées très facilement. Une amélioration a été obtenue grâce à l'amortissement du soufflet par un matériau élastomère. Par la suite la modification du système de transfert a permis d'alléger la masse reposant sur le microscope. L'amplitude des déplacements pointe-échantillons a donc encore été diminuée.

SUITE